Рис. 8
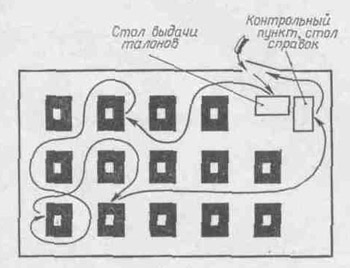
Организация "лабиринта"
"Лабиринт" проводится в классной комнате. Парты или столы расставляются так, чтобы можно было свободно ходить между ними (рис. 8).

Рис. 8
На каждый стол ставится картонный куб, на всех гранях которого (кроме основания) написаны числа и задания (рис. 9).

Рис. 9
Игра проходит так. При входе в лабиринт ученик получает талон с написанным на нем числом (например, 50). Получив талон, находит куб, на одной из граней которого написано это число, и выполняет указанное там задание (найти 20% этого числа). Результат действия (ответ задачи) он должен найти на грани другого куба и снова выполнить написанное задание и т. д. После решения нескольких заданий, количество которых указывается заранее (например, пройти 5 кубов, т. е. выполнить 5 заданий), ученик подходит к контрольному пункту и сообщает ответ. Если цепочка заданий (упражнений) выполнена правильно, без ошибок, то ответ совпадает с контрольным числом, и ученик считается прошедшим лабиринт.
Если же при выполнении одного из заданий ученик сделает какую-либо ошибку, то он может пойти по ложному пути, его ответ не совпадет с контрольным числом, и лабиринт будет считаться не пройденным; ученик должен возвратиться и постараться исправить свою ошибку, чтобы найти верный путь.
Ученик, не нашедший ошибку или встретившийся при прохождении лабиринта с "непреодолимыми" трудностями, может обратиться в стол справок. Стол справок в этой игре имеет большое обучающее значение. Ответы здесь не даются. Для каждой задачи заранее продумываются вопросы, указания и вспомогательные задания, направляющие учащегося на правильный путь решения задачи.
Например:
1. Вспомни, как решается такая задача? (Дается задача, решенная раньше.) Нельзя ли использовать ее решение?
2. Подумай, как решается такая задача? (Дается задача, составляющая часть данной задачи.)
3. Можно ли решить эту задачу, если узнать, какую часть от всех денег составляет 20 руб.? Найди эту часть.
4. Тебе нужно доказать равенство отрезков.
Подумай, нельзя ли эти отрезки включить в треугольники и доказать их равенство и т. д. Такие справки только направляют мысли учеников, заставляют вспомнить пройденное и применить его к новой ситуации.
Количество заданий может быть различным и определяется многими факторами: целью лабиринта, наличием времени, его содержанием по степени трудности заданий, составом играющих и т. д. Как правило, оно колеблется от 3 до 5.
В игре одновременно могут участвовать от 15 до 25 человек. Большее количество участников может создать скученность, что отразится на продуктивности выполнения заданий.
Для организации проведения одного лабиринта достаточно иметь 15-20 кубов крупных размеров с ребром порядка 20 см. Ради простоты хранения их лучше сделать в виде разверток, чтобы можно было складывать после проведения игры (кубы выбраны ради простоты изготовления и хранения. Внешне лабиринт будет еще привлекательнее, если изготовить различные многогранники: призмы, усеченные пирамиды, правильные многогранники и др.).
Изготовление кубов лучше выполнить так: дать каждому ученику задание вырезать из картона квадрат со стороной 20 см, для аккуратности окантовать, а затем на одну сторону наклеить квадрат из белой бумаги размером 19 см Х 19 см. Из сделанных таким образом заготовок (граней куба) нетрудно составить развертку путем склеивания их полосками марли или любого другого материала (рис. 10).
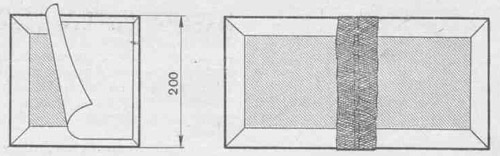
Рис. 10
Для того чтобы кубы можно было использовать для лабиринтов, различных по содержанию, на боковые грани приклеиваются уголки, которые дают возможность менять карточки-задания, т. е. изменять содержание лабиринта (рис. 11).
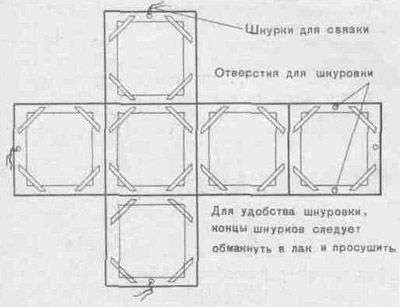
Рис. 11
Составление лабиринтов и методика их проведения
Составление лабиринта не представляет особых трудностей. Он может быть составлен по отдельной теме школьной программы, по отдельному ее разделу. Наиболее простой способ построения системы заданий для лабиринта состоит в том, что выписывают набор задач (например, состоящий из 75 задач, если мы имеем в наличии 15 кубов), группируют их по 3-5 (в зависимости от предполагаемого количества заданий), располагая задачи каждой группы по степени нарастания трудности.
Например, нужно составить геометрический лабиринт по теме "Треугольники". Составляем набор необходимых задач и группируем их по три. Например:
1. Сколько отрезков на рисунке? (6)
![]()
2. Внешний угол при вершине равнобедренного треугольника равен 80o. Найти угол при основании. (40o)
3. Дано: AB = BC = CA = CD, CD – продолжение AC. Найти Рx. (30o)
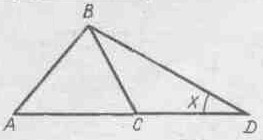
1. Сколько треугольников на чертеже? (8)
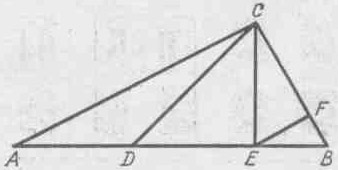
2. Углы треугольника относятся как 3:7:8. Найти разность большего и меньшего углов. (50o)
3. Дано: AB ^ BC; BC = AB; CD = CE; РBCD – развернутый; РACE – развернутый. Найти Рx. (67o,5)
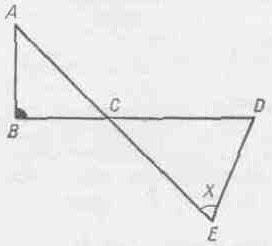
Ответы всех задач по порядку пишем крупно на карточках размера 102 мм X 144 мм, а затем под ответом первой задачи пишем вторую задачу, под ответом второй - текст третьей задачи и т.д., наконец, под ответом последней - содержание первой задачи. Получаем набор карточек (рис. 12).

Рис. 12
Заготовленные таким образом карточки перемешиваются и вставляются в грани кубов. Лабиринт готов.
Так, например, один ученик пусть получает талон, на котором написано 60. Это означает, что он должен найти это число на грани одного из кубов и решить написанное там задание. Ответ (6) должен найти на грани другого куба и решить следующее задание (ответ 40) и т. д.
Таким образом, получается цепочка чисел
| — |
| — |
| — |
| , |
Первое число - число-задание, последнее - контрольное число (Контрольное число одного ученика является номером задания для другого), показывающее, что лабиринт пройден правильно.
Перечень таких цепочек-чисел для каждого входа должен быть составлен для контрольного пункта. Наличие перечня позволяет следить за успешностью прохождения лабиринта отдельными учащимися, быстро определять правильность его прохождения.
По такому способу составляются и проводятся разнообразные лабиринты: лабиринты графиков, лабиринты фигур, геометрические лабиринты, лабиринты смекалки и т. д. Вычислительные лабиринты могут составляться несколько иначе. Упражнения здесь могут быть составлены так, что каждое следующее задание (операция, действие) выполняется над ответом предыдущего. В качестве примера приведем кусочек цепочки алгебраического лабиринта по разделу умножения степеней и возведение степени в степень (рис. 13).
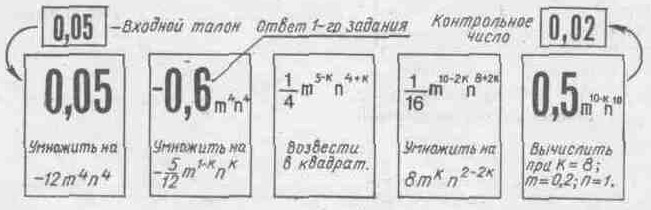
Рис. 13
Игра "Математический лабиринт", как правило, не соревнование, рассчитанное на быстроту, а серьезное занятие. Основная цель игры - повторить раздел, закрепить навыки в решении задач. Игровая форма здесь является лишь средством побуждения у учеников известного желания решить задачу, настроить их на серьезную работу, требующую проявления внимания, воли, настойчивости. Лабиринт является своеобразной проверкой личных качеств учащихся, их умений и навыков. На такую работу и нужно ориентировать учеников, чтобы при прохождении лабиринта не было спешки, торопливости. Плакат: "Поспешишь - людей насмешишь"- тоже должен предостерегать от этого учащихся.
Лабиринт рассчитан на самостоятельное решение заданий и он выгодно отличается от обычных форм самостоятельной работы: во-первых, тем, что здесь имеется дополнительный мотив, пробуждающий активность мыслительной деятельности учащихся - игровой мотив, который для некоторых учащихся является ведущим (пройти лабиринт- их основная цель); во-вторых, он проводится в непринужденной форме, так как учащиеся могут в любое время, в случае затруднения, обратиться к учителю за помощью и советом (контрольный стол); в-третьих, в нем легко (незаметно для других) учесть индивидуальные особенности учащихся. Например, для слабых учащихся можно составить более простые варианты задач с тем, чтобы они могли при достаточных усилиях наравне с другими учащимися выйти из лабиринта.
И наоборот, одаренные ученики могут рассчитывать при прохождении лабиринта на такие "головоломки", которые заставят работать мысль в полную силу.
Игра "Лабиринт" может быть как индивидуальной, так и командной (коллективной). Правила прохождения лабиринта командами остаются в основном те же. Каждый член команды проходит лабиринт самостоятельно. Контрольные числа сообщаются капитану и суммируются. Сумма индивидуальных контрольных чисел является контрольным числом всей команды. При прохождении лабиринта разрешается помощь отстающим. Правила командной игры накладывают большую ответственность на каждого члена, ибо ошибка, допущенная одним, отражается на результате всей команды.
Контроль правильности прохождения лабиринта может быть электрифицирован. Для этого можно использовать щитки от игры "Математический огонек". Каждая команда получает номер. На стене у контрольного пункта вывешиваются щитки (по количеству команд), к пластинкам прикрепляются контрольные числа (рис. 14).
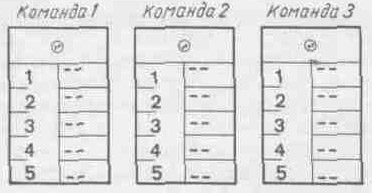
Рис. 14
Контрольные числа всего лабиринта размещаются на одном столе. Ученик, пройдя лабиринт, находит свое контрольное число (ответ последнего задания) и вставляет пластинку в ту ячейку шитка, которая соответствует его номеру в команде. Прошедшие лабиринт могут помочь своим товарищам.
Прошедшей лабиринт считается та команда, у которой вспыхнет огонек контрольного щитка (игра может носить и вид соревнования. Победителем считается тот (та команда), который первым выйдет из лабиринта и зажжет огонек контрольного щитка). Такой вид контроля доставляет учащимся большое удовлетворение.
Описанная игра является универсальной, так как может быть использована рри проведении различных внеклассных мероприятий: на занятиях математического кружка, на математических вечерах, может иметь и самостоятельное значение. Она носит не только контролирующий характер, но и обучающий, а поэтому может быть использована не только в целях проверки, но и в целях закрепления и изучения нового материала.
Прохождение лабиринта, как правило, занимает лишь часть занятия кружка или является лишь элементом математического вечера, но может быть и отдельным занятием, или даже целый вечер можно построить на основе прохождения лабиринтов.
Приведем примеры.
Лабиринт - часть занятия
Пусть темой одного из занятий кружка VI класса является "История нумераций". Занятие может быть построено по такому плану:
1. Принципы десятичной нумерации. История счета (сообщение учителя).
2. Нумерация различных народов: древняя египетская, римская, славянская (краткие выступления учеников).
3. Прохождение "Исторического лабиринта".
На этом занятии лабиринт занимает лишь часть времени и используется в целях закрепления материала темы.
Лабиринт - отдельное занятие
Планом математического кружка VII класса может быть предусмотрено несколько занятий по теме "Применение и чтение графиков". Занятия могут быть построены так:
Занятие 1.
1) Значение графиков в жизни и технике (сообщение учителя).
2) Чтение демонстрационных графиков со всем классом фронтально.
3) Самостоятельное чтение графиков.
Занятие 2. Прохождение "лабиринта графиков".
Для проведения этого занятия желательно приготовить две комнаты: одну - для подготовительной работы, условно назвав ее "Путеводителем", вторую - для размещения лабиринта.
Занятие кружка начинается в "Путеводителе". Учитель сообщает цель занятия и кратко напоминает правила прохождения лабиринта, после чего учащимся предлагается самостоятельно познакомиться с теми трудностями, которые им встретятся. На стены класса вывешивается ряд демонстрационных графиков (аналогичных графикам лабиринта) и вопросы к ним (рис. 15 а, б).
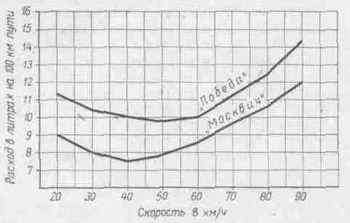
Рис. 15a
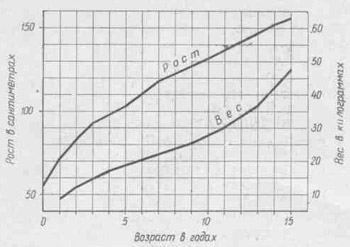
Рис. 15б
Ученики подходят к графикам и самостоятельно читают их, решают задачи. При затруднениях обращаются к учителю, который в данном случае выполняет роль инструктора. В такой непринужденной беседе проходит подготовка к лабиринту. На подготовку отводится 15-20 мин, после чего учащимся предлагается пройти в лабиринт.
На этом примере видно, как можно использовать лабиринт не только в целях закрепления материала, но и изучения нового путем самостоятельной работы на протяжении всего занятия.
Лабиринты - часть математического вечера
Покажем использование лабиринтов для проведения вечера "Путешествие в царство математической смекалки" для учащихся VI класса.
Вечер-игра "Путешествие в царство смекалки" является как бы прощальным вечером с арифметикой как предметом и проводится в конце первого полугодия.
Цель - подвести итоги всей кружковой работы, еще раз раскрыть привлекательные стороны арифметики как "гимнастики ума", показать ее значение для практической деятельности.
Для проведения вечера готовятся четыре классных комнаты (одна - для "путеводителя", три - для лабиринтов) и актовый зал для игр и развлечений ("Царство смекалки").
Основой игры, как мы уже отмечали, является прохождение системы лабиринтов: "Лабиринта чисел" (исторический лабиринт), "Лабиринта фигур", "Лабиринта смекалки", что требует некоторых знаний, умений и навыков, а также знание правил игры. Организация "путеводителя" как раз и предназначена для того, чтобы познакомить учащихся с правилами игры, дать возможность самостоятельно повторить некоторые исторические сведения, решить логические задачи, задачи занимательного характера, проверить умения и навыки в выполнении измерений, т. е. дать возможность учащимся проверить свою готовность к участию в игре, подготовить себя к ней.
Оформление "Путеводителя" проводится в соответствии с ее назначением. На стенах развешиваются таблицы нумераций разных народов и задания к ним, занимательные задачи (красиво оформленные на больших форматах). На столах у стен размещаются модели параллелепипедов с вырезами и задания к ним, с тем чтобы учащиеся могли произвести непосредственные измерения с помощью линейки. На отдельный стол ставятся образцы кубов из каждого лабиринта.
Приведем примерные вопросы к таблицам нумераций:
1. Запиши год своего рождения в славянской нумерации.
2. Архимед прожил ![]() лет. Прочитайте, сколько лет он жил?
лет. Прочитайте, сколько лет он жил?
3. Найти 2% от ![]()
4. Л. Ф. Магницкий родился в MDCIXIX году. Прочитайте год рождения Магницкого.
5. Найди ![]() от
от ![]()
6. Пол-полчети составляют ![]() . Найди все число.
. Найди все число.
Задания к моделям параллелепипедов с вырезами:
1. Найди объем модели.
2. Вычисли площадь красной поверхности.
3. Вычисли площадь полной поверхности.
Работа в "Путеводителе" завершается небольшими выступлениями учащихся и учителя по теме вечера. Учащиеся могут рассказать о роли смекалки в быту, на производстве, в военном деле. Учитель раскрывает роль математической смекалки ("Смекалка и математика").
Лабиринты организуются по общему правилу и проходятся в произвольном порядке. Треть учеников начинает с "Лабиринта чисел", другая треть - с "Лабиринта фигур", остальные - с "Лабиринта смекалки". "В "Царство смекалки" проходят при наличии трех жетонов (красный, желтый, синий), которые выдаются при прохождении соответствующих лабиринтов.
"Царство смекалки" - заключительная часть вечера. Разнообразные математические игры, аттракционы, фокусы, забавы с обязательной выдачей "призов" являются наградой за успешное преодоление математических "препятствий" юными "путешественниками".
Сделать "Царство смекалки" красивым, увлекательным, полным мысли, смекалки и смеха - дело творчества юных пионеров. Организовать это творчество - дело учителя.
В приложении 1 приведены образцы наборов карточек для нескольких лабиринтов:
1. Алгебраический лабиринт.
2. Геометрический лабиринт.
3. Лабиринт смекалки.
4. Лабиринт графиков.
Примечание 1. Особенностью лабиринтов графиков и фигур является то, что в них мы имеем дело с моделями или графиками. Поэтому график или модель кладутся на верхнюю грань куба, а карточки-задания к ним помещаются на боковых гранях этого же куба (рис. 16).

Рис. 16
Примечание 2. "Лабиринт смекалки" может быть использован в качестве своеобразной викторины, которую мы назвали "Лабиринт - викторина". Викторина проводится так.
Каждый участник викторины получает входной талон и начинает прохождение лабиринта. Если он сумеет пройти первый куб, то получает 1 очко, два куба - 3 очка, три куба-10 очков, 4 куба - 25 очков. Каждый участник не обязательно должен проходить до четвертого куба, а может ограничиться только двумя или тремя (если ему не под силу справиться с очередным заданием), а затем он имеет право взять второй, третий, ... талоны и пройти еще несколько кубов.
Выигрывает тот, кто за определенное время наберет большее количество очков.
(Образцы карточек-заданий см. в приложении 5 таблицу 28.)
© Е.А. Дышинский (разработка учебных материалов), 1960-1970
© О.А. Леонтьева, С.А. Меньшикова (вёрстка), 2002
© А.П. Шестаков (подготовка к размещению в Internet), 2002