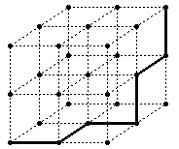
Дан фрагмент кубической кристаллической решетки с длиной ребра N. Очевидно, что кратчайший маршрут из одной вершины куба в противоположную, проложенный по ребрам решетки, имеет длину 3*N (на рисунке приведен один из возможных маршрутов для N = 2).
Технические требования:
Входной файл: INPUT.TXT Выходной файл: OUTPUT.TXT
Ограничение по времени: 5 секунд (на компьютере с процессором Pentium-100).
1) «Матрёшки» (составитель — А.П. Шестаков, оппонент — Е.В. Брызгалов) — 10 баллов.
Множество из N (N <= 15) прямоугольных параллелепипедов задано измерениями этих параллелепипедов (длина и ширина основания, высота).
Нужно сделать так, чтобы параллелепипеды были вложены друг в друга как «матрешки». При вложении стороны параллелепипедов располагаются параллельно и перпендикулярно друг другу; параллелепипеды могут быть повёрнуты, чтобы разместиться в очередном.
Требуется написать программу, указывающую порядок вложения параллелепипедов или сообщающую об отсутствии решения задачи.
Примечание. Параллелепипеды ограничены каркасом ненулевой толщины. Это означает, что, например, параллелепипед размером 10 × 11 × 12 не может быть помещён в параллелепипед размером 10 × 11 × 13.
Формат входных данных:
первая строка — N; в каждой из следующих N строк — три действительных числа — измерения соответствующего параллелепипеда.
Формат выходных данных:
Строка, содержащая N чисел, — номера параллелепипедов исходной последовательности в порядке вложения параллелепипедов друг в друга, начиная с большего, или сообщение «NO».
Пример 1 входных данных
3 1 2 3 10 30 20 5 6 8
Пример 1 выходных данных
2 3 1
Пример 2 входных данных
3 1 2 40 10 30 20 5 6 8
Пример 2 выходных данных
NO
2) Система счисления (автор-составитель — Брызгалов Е.В., оппонент — Еремин Е.А.) — 10 баллов.
Задан пример на сложение двух чисел, выполненный в позиционной системе счисления с основанием, не превосходящим 36. Запись примера имеет вид A + B = C, где A, B и C — числа, записанные в данной системе счисления.
Требуется написать программу, определяющую минимальное основание этой системы.
Технические замечания:
Цифры в системах, основание которых больше 10, обозначаются латинскими заглавными буквами: A — 10, B — 11, …, Z — 35.
Операнды и результат — натуральные числа, десятичная запись которых не превосходит 30000.
Формат входных данных:
одна строка, содержащая запись примера.
Формат выходных данных:
Одно число — минимальное основание системы счисления, при котором входное равенство является верным.
Пример 1 входных данных
2+2=4
Пример 1 выходных данных
5
Пример 2 входных данных
3A+2B=60
Пример 2 выходных данных
21
3) Встреча исполнителей (автор-составитель — Еремин Е.А., оппонент — Брызгалов Е.В.) — 12 баллов.
На квадратном клетчатом поле 10 × 10 находятся два одинаковых исполнителя: исполнитель А — в левом нижнем углу с координатами (0, 0), и исполнитель В — в правом верхнем углу с координатами (9, 9).
Система команд исполнителей состоит из следующих команд:
R — сместиться на соседнюю клетку вправо;
L — сместиться на соседнюю клетку влево;
U — сместиться на соседнюю клетку вверх;
D — сместиться на соседнюю клетку вниз.
Для сокращения записи алгоритмов разрешается объединять одинаковые следующие друг за другом команды в виде NK, где 1 < N < 10 — число повторений команды, а K — повторяемая команда (например, запись 4U эквивалентна четырем командам U, т.е. UUUU).
Выход за пределы поля любого исполнителя является ошибкой и приводит к аварийной ситуации, что прерывает все дальнейшие действия.
Каждый исполнитель получает свою собственную программную строку (считать, что она не содержит синтаксических ошибок) и исполняет ее. Будем предполагать, что на каждом шаге алгоритма исполнители выполняют по одной команде. Тогда описанная процедура закончится одним из трех способов:
1) исполнители встретятся на одной клетке поля и остановятся: в этом случае необходимо напечатать номер шага алгоритма и координаты клетки встречи X и Y;
2) у обоих исполнителей закончатся строки с программами, но встреча не состоится: в этом случае необходимо вывести на экран слово "no" — нет решения;
3) любой исполнитель выйдет за пределы поля: в этой аварийной ситуации надо напечатать слово "error" — ошибка.
Технические замечания:
1. Длина каждой из двух вводимых строк с алгоритмами для исполнителей А и В не превышает 10 символов;
2. Строки не содержат никаких других символов, кроме цифр и букв R, L, U и D.
Формат входных данных:
2 строки, содержащие программы для исполнителей A и B.
Формат выходных данных:
Три числа — номер шага алгоритма, на котором произошла встреча и ее координаты, или сообщения no либо error.
Пример 1 входных данных:
9U9R 9L9U
Пример 1 выходных данных:
9 0 9
Пример 2 входных данных:
U4U D4D
Пример 2 выходных данных:
no
Пример 3 входных данных:
U2U D3U
Пример 3 выходных данных:
error
4) Неубывающие последовательности (автор-составитель — Гладков В.П., оппонент — Шестаков А.П.) — 18 баллов.
Пусть все неубывающие последовательности длины k (1 < k <= 25), содержащие числа из отрезка [1; k], такие, что соседние элементы отличаются не более, чем на 1, расположены в лексикографическом порядке. Например, для k = 4, получаем: 1111, 1112, 1122, 1123, 1222, 1223, 1233, 1234.
Требуется написать программу, которая по заданным k и n выводит n-ую последовательность длины k или указывает, что последовательности с таким номером не существует.
Формат входных данных:
В единственной строке входного файла содержатся два целых числа, разделенные пробелом: k n. (1 < k <= 25, 1 <= n <= 230.)
Формат выходных данных:
В единственной строке должна содержаться искомая строка или быть записана фраза «NO».
Пример входных данных:
4 5
Пример выходных данных:
1222
5) Кубик (автор-cоставитель — Брызгалов Е.В., оппонент — Деменев А.Г.) — 20 баллов.
Дан фрагмент кубической кристаллической решетки с длиной ребра N. Очевидно, что кратчайший маршрут из одной вершины куба в противоположную, проложенный по ребрам решетки, имеет длину 3*N (на рисунке приведен один из возможных маршрутов для N = 2).
Требуется написать программу, определяющую количество таких маршрутов.
Формат входных данных:
Одна строка, содержащая натуральное число N <= 100.
Формат выходных данных:
Одна строка, содержащая число всевозможных кратчайших маршрутов.
Пример входных данных:
2
Пример выходных данных:
90
6) Четырехугольник (автор-составитель — Брызгалов Е.В., оппонент — Деменев А.Г.) — 30 баллов.
На клетчатой бумаге изображен выпуклый четырехугольник, вершины которого находятся в узлах сетки.
Требуется написать программу, определяющую количество узлов сетки, которые являются внутренними точками четырехугольника (узлы-вершины и узлы, лежащие на сторонах четырехугольника, внутренними точками НЕ являются).
Четырехугольник задается координатами вершин, перечисленных в порядке обхода по (или против) часовой стрелки. Координаты по абсолютной величине не превосходят 10000.
Формат входных данных:
4 строки, каждая из которых содержит два целых числа, разделенных ровно одним пробелом, — координаты одной из вершин четырехугольника.
Формат выходных данных:
Одна строка, содержащая число узлов сетки внутри четырехугольника.
Пример входных данных:
3 3 4 4 3 5 2 4
Пример выходных данных:
1
© Пермский областной Оргкомитет олимпиад школьников по информатике, 2001